最近在學3D圖形學...看到篇不錯的視錐剔除入門教程,於是搬來翻譯了...原文:http://www.flipcode.com/archives/Frustum_Culling.shtml
時至今日,許多剛剛下海的3D引擎程序員仍不了解視錐剔除(Frustum Culling)的重要性和益處,這讓我和我的小夥伴們感到很震♂驚.我在Flipcode的論壇中發現儘管網絡上有海量的相關資料,仍有許多人提出對視錐剔除實現的問題.因此我決定撰寫這篇文檔,簡單描繪出我現在所使用的四叉樹剔除引擎(Quad-tree Culled Engine)的工作方式.誠然,市面上有許多種成熟且高效的視錐剔除算法,但我認為這個算法足以用來學習視錐剔除的理論基礎.在正式開始前我還想說明一件事,以前我一直把Frustum(平截頭體)打成Frustrum(截頭錐),為此我沒少被論壇上的人噴.在這裡我承認Frustum是正確的拼寫.對那些以前被我冒犯的人我表示抱歉...你們這群吹毛求疵的傻[嗶-]...
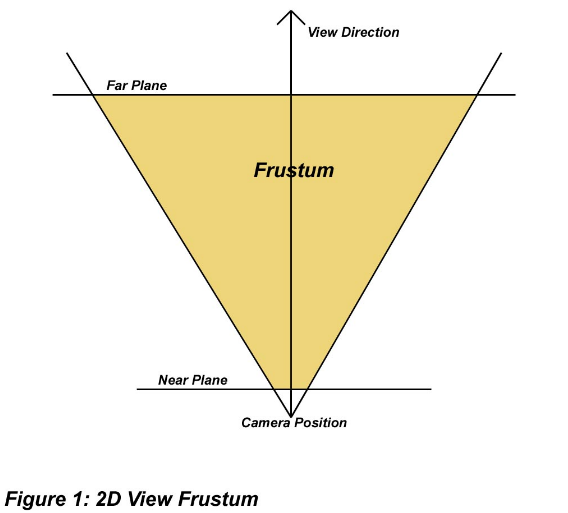
大多數人已經知道什麼是視錐剔除了(譯者:如果你是手滑誤點進來的...視錐剔除是一個圖形渲染前的步驟,用於剔除掉不需要繪製的部分).視錐(準確說是平截頭體Frustum)的形狀酷似一個塔尖被削平了的金字塔,更準確地說,是一個四稜錐的頂點偏下位置被一個裁面(Clipping Plane,見圖1)裁斷.事實上,視錐本身就是由6個面所組成.這6個面被稱為近裁面,遠裁面,上裁面,下裁面,左裁面,右裁面.視錐剪裁僅僅是一個用來判斷物體是否需要被繪製的過程.儘管從本質上講視錐剔除應該是三維層面的,但事實上大多數時候它僅僅需要以純代數的方法便能解決.這也是為什麼我如此推崇視錐剔除的原因,它非常的快(如果算法好的話),而且是在渲染管線(Rendering Pipeline)之前進行的,不像背面剔除(Backface Culling)那樣需要在渲染管線之後一個頂點一個頂點地計算.對於被剪裁掉的物體繪圖引擎都不會將其送入顯卡(譯者:那是...被剔除掉的壓根都不用渲染),因此視錐剔除對渲染速度有巨大的改善,畢竟什麼都不渲染是最快的渲染.
然而,視錐剔除的高效還得益於它背後的算法,分層剔除法(Hierarchy Culling Method)是一種很好的算法.該算法將一個三維世界分割為一個樹型結構,一旦我們剔除掉一個節點,那麼那個節點往下的子節點就也被一併剔除了.這樣我們就不必一個個剔除三維世界中每一個物體.我們只需簡單地分層處理便能成倍地剔除物體,省下了大量的剔除計算時間.若不使用分層法,視錐剔除就必須以最少O(n)的時間複雜度一個個判斷物體是否需要繪製,換句話說,100個物體需要100次計算,1000000個物體就需要1000000次!儘管進行視錐剔除總比不進行好,但糟糕的算法卻會使我們的努力變得不那麼明顯.若要製作出一個優化良好的遊戲,能使用一個O(lgN)甚至O(c)的算法就不要使用一個O(n)的算法,我是絕不接受後者的,因此我選擇了分層剔除法.想象一下,這裡有100個物體,但只有1個位於我們的視野內,如果我們使用二分法來剔除的話,原本需要100次計算的線性算法,現在只需要7步(100->50->25->13->7->4->2->1,作者原文寫的6步...).O(n)與O(lgN)的區別,很容易就能看出來.
我的分層剔除法使用四叉樹分層.一個二叉樹或八叉樹或隨便什麼結構其實都可以勝任這個工作.事實上,代碼很容易移植.我選擇四叉樹是因為它非常直觀.本質上四叉樹是一個二維平面上有4個節點的樹(見圖2).因此,每一個子節點都剛好是父節點的平面中的一個象限.因此我們認為它是"分層的",每一個子節點都在父節點之內,如果我們認定一個父節點是不可見的,我們便也可以斷定子節點同樣是不可見的.因此我們可以以飛快的速度處理海量的物體數據,特別是對於擁有數十萬頂點數據的地形渲染引擎.而且它具有擴展性,地形上的裝飾物可以被加進最小的四叉樹節點當中.

基本方法1
要規劃一個視錐剔除系統的第一步是確保你已經有合適的剔除算法,這意味着我們需要先知道如何根據視角/投影矩陣(View/Projection Matrices)通過6個平面構建出一個平截頭體,同時還要讓它既能檢測球體也能檢測立方體.說的更簡單一點,我們得知道判斷一個球體或立方體與平截頭體是包含、相交還是外離的方法.這可以讓我們待會將要製作分層剔除法更加完善.
首先讓我們來定義我們的平截頭體.平截頭體的6個面可以根據我們使用的渲染API(Direct3D/OpenGL)的鏡頭系統的視角/投影矩陣來定義.在不同的渲染API中定義起來有些差別.我嘗試為Direct3D和OpenGL各寫一份,但我最後發現這樣只能讓讀者越來越困惑.幸運的是我的一位朋友已經寫了一份很好的教程.回到1996年,我參觀Raven公司時遇見了吉爾,那時我幾乎已經是鐵定被簽約下來,到Raven和吉爾一起工作,但NAFTA(北美自由貿易協定)卻阻止我這樣沒有大學文憑的人跨國工作.NAFTA我去年買了個登山包!超耐磨!不管怎麼說,這是題外話.最重要的是那份教程清晰地描述了如何從矩陣中提取出6個裁面來.我建議你仔細讀讀並理解它:
http://www2.ravensoft.com/users/ggribb/plane%20extraction.pdf
(譯註:這個網址已經訪問不了了,可以試試這個http://www.cs.otago.ac.nz/postgrads/alexis/planeExtraction.pdf)
現在我假定你已經編寫好了一個通過6個裁面定義的平截頭體類,為了提高效率,請將其設計為僅在視角/投影矩陣發生改變時(換句話說,鏡頭髮生移動時)才進行重構,而不是每一幀都重構一次.接下來我們要設計判斷一個球體與平截頭體是內含、相交還是外離的算法(譯註:內含和相交有什麼區別?等看到章節"優化1"時你就明白了).這其實非常簡單:遍歷6個裁面,判斷球體是在該裁面的正面,背面,還是相交,實現起來確實不難,我們需要計算從球體中心到該裁面的距離.如果距離的絕對值小於球體半徑,那麼就是相交.如果距離大於0那就是在裁面正面(有可能在平截頭體內).如果小於0那麼就是在裁面背面.計算方法是:
設C(Center)為球中心坐標
設N(Normal)為平面法線向量
設D(Distance)為坐標系原點到裁面的距離
則計算公式為:距離=(C向量點乘N)+D,即C·N+D
(譯註:由於C和N同維數,所以C與N可以直接點乘.我剛開始看到這個公式時很暈乎,後來百度出一篇高中教案,其中寫道"利用法向量求點到平面的距離...把點A到平面的距離看成點A與平面內任意一點B所構成的向量在法向量方向上的投影的長度...",這便是C·N的出處,由於坐標系原點不一定在我們的裁面上,所以最後還要+D來修正一下.順便一提那教案結尾還加了一句"此方法無需技巧,人人都會",我去年買了個表.)
正如我之前說的那樣,再往下我們所需要做的就僅僅只是判斷距離與球體半徑的大小關係.這裡是我編寫的C++代碼:
///判斷某球體是否在平截頭體內
int Frustrum::ContainsSphere(const Sphere& refSphere) const
{
//球體中心到某裁面的距離
float fDistance;
//遍歷所有裁面並計算
for(int i = 0; i < 6; ++i)
{
//計算距離
fDistance = m_plane[i].Normal().dotProduct(refSphere.Center())+m_plane[i].Distance();
//如果距離小於負的球體半徑,那麼就是外離
if(fDistance < -refSphere.Radius())
return(OUT);
//如果距離的絕對值小於球體半徑,那麼就是相交
if((float)fabs(fDistance) < refSphere.Radius())
return(INTERSECT);
}
//否則,就是內含
return(IN);
}
接下來就是(在四叉樹中)判斷一個軸對齊包圍盒(Axis-aligned Bounding Box,簡稱AABB,不是BBA哦...說白了就是一個邊平行於坐標軸的立方體)與平截頭體的關係.對於這步操作有數種方法.首先是包圍盒(Bounding Box,指一個多用於碰撞檢測的有邊界的立方體,AABB包圍盒是最簡單的一種)的定義,我的包圍盒是由2個坐標組成,分別代表"最小(靠近坐標軸負方向)"頂點和"最大"頂點,為了壓縮體積,我乾脆將它的數據結構設計為連續的6個數,接下來便是將包圍盒的8個頂點依次與平截頭體作對比,儘管這種做法不是最快的一種,但它卻是最容易實現,最容易被學會的一種.我們只需要測試每一個頂點(立方體的角)與平截頭體的關係即可.如果所有的點都在平截頭體內,那這個立方體就是被包含;如果有1~7個點在裡面,就是相切;如果所有的點都在某一個裁面的背後,那就是外離;否則,就還是相切,為什麼?很好,因為有可能立方體沒有一個點在平截頭體內,但依然和平截頭體相切(譯註:比如平截頭體的一個"尖"恰好插入立方體內).事實上,我們仍沒有考慮一種極端情況:有一個超大的包圍盒將平截頭體整個包裹起來了,按我們現在的算法它是相交,事實上它真的是相交嗎?這種情況我們會在章節"優化1"中討論.
檢測一個點是否在平截頭體內也依舊簡單到不需要媽媽擔心.我們只需要將它和6個裁面作對比,判斷它是在每一個裁面的正面就行(作者:別忘了,我們的裁面都是面向平截頭體內部的. 譯者:我去年買了個表,你之前有說嗎?).判斷點和裁面的關係其實和判斷球體和裁面的關係一樣...依然是萬金油公式:C·N+D.如果結果大於0,就是在正面.如果小於0,就是在背面.如果是0就說明是在面內.除非你設計的算法有特殊的要求,不然我建議你僅需簡單地將其等價視為在正面.(另外,如果你真的需要判斷點是否是在面上的話,請記住絕對不要直接用等於號判斷,別忘了浮點精度啊...).儘管聽起來它和球體判斷是一樣的,但我仍不介意再重寫一遍,下面是代碼:
///判斷AABB盒是否在平截頭體內
int Frustrum::ContainsAaBox(const AaBox& refBox) const
{
Vector3f vCorner[8];
int iTotalIn = 0;
//獲得所有頂點
refBox.GetVertices(vCorner);
//測試6個面的8個頂點
//如果所有點都在一個的背後,那就是外離
//如果所有點都在每一個面的正面,就是內含
for(int p = 0; p < 6; ++p) {
int iInCount = 8;
int iPtIn = 1;
for(int i = 0; i < 8; ++i) {
//測試這個點
if(m_plane[p].SideOfPlane(vCorner[i]) == BEHIND)
{
iPtIn = 0;
--iInCount;
}
}
//所有點都在p面背後嗎?
if(iInCount == 0)
return(OUT); //外離
iTotalIn += iPtIn;
}
//如果iTotalIn是6,那麼就都是在正面
if(iTotalIn == 6)
return(IN); //內含
return(INTERSECT); //相交
}
好了,這就是視錐剔除的主要部分,你還好吧?
優化1
第一個對上面的函數的優化的方式非常簡單.如果你仔細研究了那兩個函數,你會發現球體檢測比立方體檢測要快很多.這意味着我們最好盡量使用球體檢測而不是立方體檢測,或者用球體檢測進行預預判,判斷通過後再使用立方體檢測進行詳細判斷,有時我們使用立方體作為物體的渲染範圍是因為它更匹配物體的形態,但我仍推薦先使用球體進行預判斷,然後再用立方體判斷.事實上,我現在使用的遊戲引擎為每一個渲染目標同時分配了球體和立方體兩個渲染範圍.它們都在同一個四叉樹節點上,在判斷時前者優先於後者,這樣我就可以用球體判斷來快速剔除掉大量的節點/物體,然後再使用立方體判斷仔細篩選.這一種簡單的優化僅需要犧牲一點點內存空間便能提升性能.你所需要的僅僅只是為每一個物體分配兩個渲染範圍判定.
下一個優化是選擇一種最優的分層結構遍歷方式.以我們使用的四叉樹為例,傳統方法是檢測一個父節點是否為可見的.如果是,那麼就去檢測每一個子節點.如果不是,那麼就停止處理.說白了這就是對每一個節點進行遞歸處理.一旦我們遍歷完成並決定出了需要繪製的節點,我們便將那些節點的內容送往顯卡進行渲染.但想象一下,對於一個尚未完結的節點(一個有子節點的節點),如果這個節點是全部可見的,那麼我們還需要檢查它的子節點嗎?既然它已經是全部可見的了,那麼它的子節點也一定是可見的,再對它們進行判斷就只是浪費你的CPU了!這就好比你不會去處理那些絕對不可見的節點一樣.明白為何我們之前要判斷"內含,相交,外離"而不是簡單的"包含,不包含"了吧?對於完全不可見的節點,我們只需簡單地剔除掉即可,對於全部可見的節點,我們也只需簡單地放行即可,真正需要進一步遞歸處理的是部分可見而部分又不可見的節點,也就是那些"相交"的節點.這一步優化又能提升不少性能.
第三項優化則是如果鏡頭位於某個節點的渲染範圍內部的話,就直接視為檢測通過並開始檢測它的子節點.這種情況可以被視為相交,我們只需要開始檢測子節點就行了.我的實現方法是如果判斷鏡頭位於一個立方檢測盒內部的話,就直接按照相交來處理.如果採用了這個優化,那麼你的四叉樹遞歸函數應該類似於這樣:
///對節點的遞歸處理
void QuadTree::RecurseProcess(Camera* pPovCamera, QuadNode* pNode, bool bTestChildren)
{
//在裁剪前是否需要檢測?
if(bTestChildren) {
//首先檢測是否是在檢測盒內
if(pNode->m_bbox.ContainsPoint(pPovCamera->Position()) == NOT_INSIDE)
{
//先進行球體檢測
switch(pPovCamera->Frustrum().ContainsSphere(pNode->m_sphere)) {
case OUT:
return;
case IN:
bTestChildren = false;
break;
case INTERSECT:
//檢測立方體是否在視角內
switch(pPovCamera->Frustrum().ContainsAaBox(pNode->m_bbox)) {
case IN:
bTestChildren = false;
break;
case OUT:
return;
}
break;
}
}
}
//[在這裡填入判斷代碼]
}
基本方法2
如果你已經實現了上述所有的內容,並且注意觀察你的程序的性能的話,你應該會注意到相交判斷代碼依然有些冗雜,它們佔了CPU運算的大頭.當然具體程度取決於你的程序中的物體數,以及你的四叉樹的深度,和各種各樣的因素.就算不進行性能分析,光憑眼睛看也會發現相交判斷代碼十分的複雜.就算是相對最快的球體檢測也依舊需要檢測球心和數個面的關係,最好情況下也至少得有1個,最糟情況下需要和全部6個面進行檢測.不過這還有改善空間.先讓我簡單闡述一下接下來我們要做的.
第一個是球-球相交檢測.這個檢測又快又簡單.只需要計算兩個球體的球心距離然後和兩者的半徑和作對比,若距離小於半徑和則是相交(在這裡我們將內含也視為相交,因為已經沒有必要分的那麼清楚了),否則就是不想交.下面是我的算法,你應該會注意到我是使用距離的平方進行判斷,因為開根操作很慢!
///測試兩個球體是否相交
bool Sphere::Intersects(const Sphere& refSphere) const
{
//獲得一個從目標球心指向本球心的向量
Vector3f vSepAxis = this->Center() - refSphere.Center();
//計算半徑和
float fRadiiSum = this->Radius() + refSphere.Radius();
//簡單地說,如果向量的模長小於半徑的話,就是相交
//但直接求向量模長的話,需要一次開根操作
//而乘法(平方)操作遠比開跟操作要快
//所以我使用摸的平方與半徑和的平方作對比
if(vSepAxis.getSqLength() < (fRadiiSum * fRadiiSum))
return(true);
//否則就是不相交
return(false);
}
下一個是判斷球體和圓錐是否相交的算法.這個要比球-球相交判定複雜得多.我可以給你完整解釋一遍如何實現,但幸運的是,已經有人替我這麼做了.Dave Eberly(譯註:《3D Game Engine Architecture》一書的作者)已經在他的網站Magic-Software.com上撰寫了一篇完善的文檔,用以解釋球-圓錐相交判定的算法.
譯者:事實上,Magic-Software.com似乎已經易主了...原文中的鏈接也自然不在了,你可以在百度文庫中找到一個副本:
http://wenku.baidu.com/view/6388b482e53a580216fcfe9c
我認為這個網站是一個超棒的資料庫,裡面有大量的代碼和文檔(譯者:可是TMD已經不在了啊...).他的文檔即詳細解釋了原理,又給出了完整的代碼.事實上,如果你沒有雄厚的數學背景的話,你也可以簡單地把結尾的代碼複製然後直接使用.雖然我不推薦這樣做,但有些人就是不能徒手將自然底數算到小數點後第⑨位,對於像譯者那樣的數死早,我只能說呵♂呵.那麼現在我們已經有了兩個高貴上檔次的新算法了...可它們能用來幹啥?很好,這就是下一章的內容...
優化2
Yep,你猜到了.那兩個算法是用來進一步優化我們的視錐剔除算法的.正如我在上一章的開頭所說,平截頭體檢測其實是很慢的,能避免的話就不要進行與它相關的操作.你應該也注意到球-球檢測和球-錐檢測要比平截頭體檢測要快一些.所以我們可以把它們作為預檢測算法,利用它們的高速,提前剔除掉那些根本不可能相交的物體,僅讓可能相交的物體進行平截頭體檢測.接下來我們要做的是為平截頭體構建一個球體和圓錐.之後在檢測時,我們讓物體的渲染判定球和平截頭體的球進行檢測,通過後再與圓錐進行檢測,依然通過後則再與平截頭體進行檢測.這種算法看上去很麻煩,其實對計算機而言計算起來遠比直接檢測平截頭體要快得多.
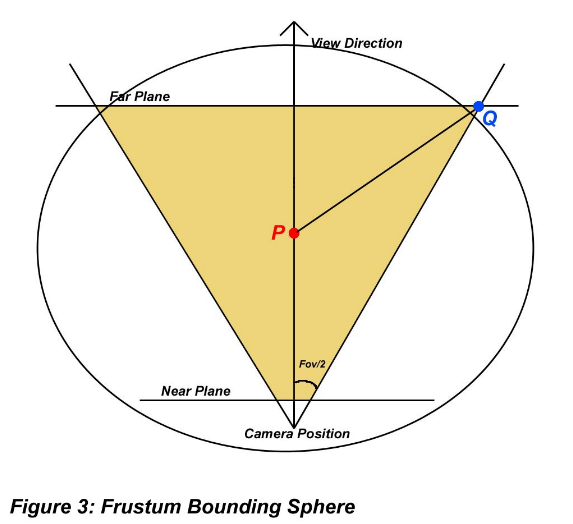
創建一個包裹着平截頭體的球體並不難(譯者:尼瑪我怎麼就不會...),但創建一個合適的圓錐就不容易了.創建球體的方法是讓球的球心位於平截頭體的中央,讓它的半徑能夠剛好到平截頭體的遠角(遠裁面的任意一個角).為什麼是遠角?好吧,平截頭體其實不就是一個向外擴張的被砍掉頭的稜柱嗎?無論你的視野再怎麼遠,也遠不過平截頭體的遠角,換句話說,如果半徑能夠到它,那麼球體就能完整地包裹下整個平截頭體.你也許會問為何不是近角(近裁面的角),這給就是純幾何問題了,請看圖3.定位球體中心位置的過程毫不費力.將近裁面與遠裁面之間中間的那個點定為中點就足夠了.而計算球體半徑有一點小難.通常平截頭體是由FOV(視野範圍,一個角度,通常為75)決定.利用FOV,我們能通過幾何方法計算出從球心到遠角的距離.我們將原點定為鏡頭位置,X軸Y軸定為與近/遠裁面平行,Z軸定為從原點指向遠裁面中點的方向.將P點定為球心,Q定為一個遠點,則P可以被表示為(0,0,nearClip + ((farClip + nearClip) / 2)),其中nearClip和farClip分別為原點到近裁面和遠裁面的距離.下面是我的代碼:
//計算平截頭體球的半徑 //首先計算遠裁面與近裁面的距離 float fViewLen = m_fFarPlane - m_fNearPlane; //計算遠裁面的高,這裡有個問題,FOV通常是從視角原點開始算的,這裡應該用m_fFarPlane而不是fViewLen才對,作者的筆誤? float fHeight = fViewLen * tan(m_fFovRadians * 0.5f); //在橫縱比為1時,寬和高一樣,否則還要再計算寬... float fWidth = fHeight; //確定P點 Vector3f P(0.0f, 0.0f, m_fNearPlane + fViewLen * 0.5f); //確定Q點 Vector3f Q(fWidth, fHeight, fViewLen); //獲得一個半徑向量 Vector3f vDiff(P - Q); //於是球體半徑就是模長了 m_frusSphere.Radius() = vDiff.getLength(); //然後我們要確定這個球在全局坐標系中的位置 Vector3f vLookVector; m_mxView.LookVector(&vLookVector); //計算球體中心在全局坐標中的位置 m_frusSphere.Center() = m_vCameraPosition + (vLookVector * (fViewLen * 0.5f) + m_fNearPlane);
構建包圍平截頭體的圓錐則相對簡單一些.如果你讀了那篇介紹球-錐相交判定的文章的話,你應該知道一個圓錐可以通過一個頂點(圓錐的原點),一個軸射線(指向圓錐的方向)以及一個錐角(母線和軸射線的夾角)組成.圓錐的頂點就是鏡頭的原點.軸射線就是鏡頭面向的方向.唯一的難度在於錐角的計算.如果我們只是簡單地用FOV作為錐角的話,那麼我們創建出的圓錐無法包裹住平截頭體的四個遠角.所以還是要通過計算來算出一個合適的錐角.利用一些幾何學技巧,我們可以算出新的FOV.既然我們已經有平截頭體的FOV,我們就能利用勾股定理,使用舊FOV(以及屏幕的尺寸)計算出FOV三角形的臨邊,然後再用臨邊與屏幕中點到邊角的線段組成一個新的三角形,進而計算出新的FOV.聽起來有些略繁瑣,可以看下面的代碼:
// vLookVector是鏡頭的方向向量 // Position()為獲取鏡頭的位置 // fWidth為屏幕寬度的一半(單位:像素). // fHeight為屏幕高度的一半(單位:像素). // m_fFovRadians是平截頭體的FOV // 計算FOV三角形的臨邊 float fDepth = fHeight / tan(m_fFovRadians * 0.5f); // 計算從屏幕中點到邊角的距離 float fCorner = sqrt(fWidth * fWidth + fHeight * fHeight); // 計算新的FOV float fFov = atan(fCorner / fDepth); // 初始化圓錐 m_frusCone.Axis() = vLookVector; m_frusCone.Vertex() = Position(); m_frusCone.SetConeAngle(fFov);
構建完球體和圓錐後,我們就可以用它們來快速剔除物體了.(你應該注意到我沒有剔除圓錐之內、遠裁面之外的節點.這是因為大多數的這些節點已經在球-球檢測階段被剔除了.圓錐檢測主要是為了剔除平截頭體側面的節點.)這是改寫後的代碼:
///對節點的遞歸處理
void QuadTree::RecurseProcess(Camera* pPovCamera, QuadNode* pNode, bool bTestChildren) {
//在裁剪前是否需要檢測?
if(bTestChildren)
{
//首先檢測是否是在檢測盒內
if(pNode->m_bbox.ContainsPoint(pPovCamera->Position()) == NOT_INSIDE)
{
//檢測我們是否和平截頭體的球體相交
if(!pPovCamera->FrustrumSphere().Intersects(pNode->m_sphere))
return;
//檢測我們是否和平截頭體的圓錐相交
if(!TestConeSphereIntersect(pPovCamera->FrustumCone(), pNode->m_sphere))
return;
//先進行球體檢測
switch(pPovCamera->Frustrum().ContainsSphere(pNode->m_sphere))
{
case OUT:
return;
case IN:
bTestChildren = false;
break;
case INTERSECT:
//檢測立方體是否在視角內
switch(pPovCamera->Frustrum().ContainsAaBox(pNode->m_bbox))
{
case IN:
bTestChildren = false;
break;
case OUT:
return;
}
break;
}
}
}
//[在這裡填入額外的判斷和渲染代碼]
}
結論
我自認為這是一篇挺不錯的視錐剔除入門文章,我希望它能對新手圖像引擎程序員有幫助.如果你仔細讀下來的話,你也會發現本文除了譯者糟糕的翻譯以外,沒有什麼過於複雜的概念和大筆大筆的數學公式(事實上,數學公式都在引用的兩篇文章里...).誠然,我介紹的算法並非最佳的視錐剔除算法,更何況對於這種算法而言,仍有不少進一步優化的方法,但對於入門而言,它已經足夠了.如果你發現文中有含糊不清的地方的話,如果確保不是譯者犯二的話就儘管找我抗議吧!
我很感謝我的好基友Gil Gribb(譯註:Raven公司員工,參與過包括《戰爭機器》、《命運戰士》等多款遊戲的製作)和Klaus Hartmann(譯者:《哈德曼的妖怪少女》...歪樓了(づ ̄3 ̄)づ),感謝他們在裁面提取方面的優秀的文章.我也很感謝Dave Eberly在圓錐算法方面的幫助,以及他那個包羅萬象的網站(儘管已關閉)!另外,感謝Charles Bloom在網上撰寫的一篇文章,它啟發了我使用球體和圓錐來進行快速剔除.人類的最大美德莫過於知識的分享,以至於我除了發自心底地感謝那些願意將自己的知識分享給他人的人以外,別無他言.
另外記住...練習才是進步的最佳捷徑 - 百試百靈,無效退款.我(口頭)保證!
譯者:既然作者寫完了那麼就輪到我來蛋逼了!(~o ̄▽ ̄)~o 很久沒做翻譯了...上一次翻技術文章還是去年暑假...老實說在計算機圖形學我還是個猹啊,專業名詞方面我盡量做到規整,不過還是翻得有些213...好吧不多說了,撤了...ԅ(¯﹃¯ԅ)
